Algoritmos: Como medir?
No post anterior, introduzimos o conceito de Análise Assintótica e falamos brevemente sobre o Big O Notation. Nesse post, vamos pincelar sobre como mensurar um algoritmo utilizando a notação.
Mas antes de mais nada é preciso reforçar: O Big O é apenas uma das métricas (número de passos proporcional ao tamanho do seu input) que pode te levar à conclusão de que o seu algoritmo é eficiente ou não. Em momento de implementação, outras métricas como memória, tempo, acesso a recursos e consumo de energia podem impactar nesse resultado.
Para tanto, é comum termos duas formas distintas de análise:
- Empírica: Tempo de execução do código, implementado na linguagem de programação de sua escolha.
- Analítica: Não leva em consideração o ambiente no qual o seu algoritmo irá executar, representando através de uma ordem de grandeza o tempo de execução do algoritmo.
Vamos focar no método analítico, claro. Se você está interessado no método empírico, ferramentas de profiling podem te dar ótimas dicas sobre a performance da sua solução.
Tempo x Espaço
É possível utilizar o Big O para medirmos quanto de espaço que um determinado algoritmo ocupa. Na Wikipedia existe inúmeros wikis sobre algoritmos famosos, e grande parte deles apresenta a seguinte estrutura:
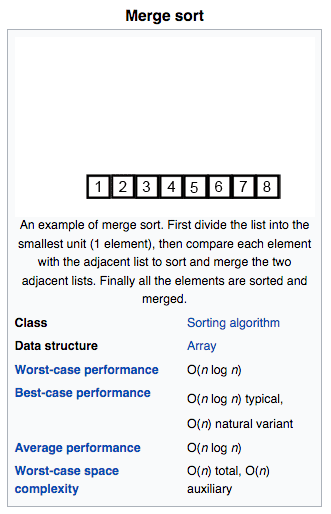
O Merge sort, um dos mais famosos algoritmos de ordenação, além de ter
uma performance média de O (n log n), em seu pior cenário ocupa
O(n) de espaço. Onde n corresponde ao tamanho da entrada do algoritmo.
Logo, se você passar um array de 10 posições para o Merge sort ordenar,
ele ocupará outras 10 posições ao fim do processo.
Em contrapartida, o Bubble sort, também famoso mas nada performático
(O(n²)), ocupa O(1) (não necessitando de novas posições na memória
para fazer a ordenação).
Se você estiver projetando a sua solução para um ambiente limitado, será necessário levar em consideração o espaço, mas é muito comum nos tempos atuais sacrificarmos memória em prol do tempo de execução.
Quanto mais próximo de linear, melhor
Voltando o foco ao tempo de execução, é possível categorizarmos um bom algoritmo quando ele é o mais próximo possível de linear (se ele for sublinear ou constante, melhor ainda). Ou seja:
- Se ordernar 10 items leva 1 milissegundo;
- Ordenar 20 items deveria levar 2 milissegundos;
- E ordenar 100 items deveria levar 10 milissegundos.
Esse comportamento é linear, resultando em O(n). Mas o comportamento abaixo
não é o dos melhores:
- Se ordenar 10 items leva 1 milissegundo;
- E ordenar 20 items leva 4 milissegundos;
- E ordenar 100 items leva 100 milissegundos;
- Temos uma progressão quadrática, resultando em
O(n²).
Algo não tão desejável em se tratando de algoritmos.
Mais um pouquinho de teoria
Vamos gastar um pouco de teoria aqui para definir Big O:
Se um tempo de execução é O(f(n)), então para um n suficientemente grande, o tempo de execução é no máximo k*f(n) para alguma constante k.
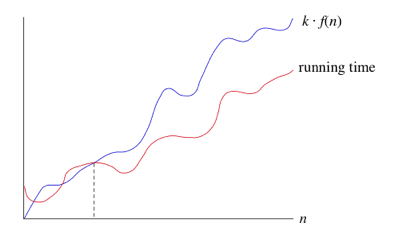
Dizemos que o tempo de execução é big-O de f(n) ou só O de f(n). Com
isso informamos limites assintóticos superiores, ou seja, que no pior cenário
o tempo de execução cresce de uma maneira até atingir determinado limite, mas
poderia crescer mais devagar. Não podemos desconsiderar que o input tem que ser
suficientemente grande (repare na linha pontilhada). Não é incomum vermos
algoritmos que performem em O(n log n) tendo um desempenho ruim com um
conjunto de dados pequeno.
Agora sim! Vamos contar
Complexidade constante: O(1)
Queremos calcular qual é a complexidade de um algoritmo de troca de valores:
def swap(num1, num2):
temp_num = num1
num1 = num2
num2 = temp_numPodemos, em teoria, contar cada atribuição de valor executada pelo algoritmo
como um “passo”. Teríamos complexidade = 3, e esse resultado nunca mudará,
não importa qual valor que passe de entrada. Logo, é possível dizer que a
complexidade desse algoritmo é constante, representada por O(1).
Pode parecer confuso não utilizar O(3), mas seguindo a definição matemática
apresentada anteriormente, quando eu assumo que meu algoritmo tem
complexidade O(1), estou dizendo que o seu limite assintótico superior é menor
ou igual a k * f(n). Se considerarmos o k como constante representando a
quantidade de atribuições do nosso algoritmo (3) e f(n) como o
running time (1), temos como upper bound o valor 3.
Em outras palavras: Se o tempo de execução do seu algoritmo é constante, a
maneira ideal de representá-lo é através de O(1).
Complexidade linear: O(n)
Quando a entrada do algoritmo é variável em tamanho, temos um comportamento diferente:
def soma(array):
total = 0
for num in array:
total = total + numGeralmente quando temos algum loop, e ele está ligado ao input, dificilmente chegamos a um algoritmo de complexidade constante. No caso acima, podemos contar os passos da seguinte forma:
n = tamanho(array)total = 0: 1 operaçãoatribuição de valor a num: n operaçõestotal = total + num: n * 2 operações
Para cada elemento do array, executaremos uma soma (total + num) e uma
atribuição (total = <resultado>). Chegamos à conclusão que
complexidade = 1 + (n * 2). Mas como chegamos a O(n)?
Deixando a parte matemática de lado, quando trata-se de análise assintótica,
estamos mais interessados no que realmente interfere na performance do
algoritmo. Ou seja, os valores constantes (1 e 2) nessa análise são detalhes
se comparados ao impacto que n causa ao tempo de execução. Portanto, uma das
maneiras de encarar a mensuração do Big O é simplesmente ignorando as
constantes e focando no que é dinâmico, nos levando a complexidade = n e em
consequência ao O(n).
Considerações finais
E como num passe de mágica, depois de certa intimidade com o Big O Notation,
você passa a assumir a complexidade de um algoritmo com uma breve “olhadela”.
Ao ver um loop assume que é n, ao ver loop dentro de loop, que é n²,
e assim por diante…
Nos próximos posts vamos explorar algoritmos de diferentes complexidades, entrando em detalhes para entender os seus tempos de execução e alternativas otimizadas.
Até a próxima!
Esse post foi originalmente escrito para o Profissionais TI.