Algoritmos de ordenação - Parte 1

Klaus Peter Laube

10 de maio de 2019 - 9 minutos de leitura

Voltamos a falar sobre algoritmos, e dessa vez o tópico é sobre ordenação de elementos. As linguagens de programação abstraem toda a complexidade envolvida para nós, mas mais que fundamental, compreender como tais algoritmos funcionam é mais um passo adiante no aprendizado das Ciências da Computação.

Definição

Algoritmos de ordenação (ou Sorting Algorithms) podem ser definidos como:

(...) an algorithm made up of a series of instructions that takes an array as input, performs specified operations on the array, sometimes called a list, and outputs a sorted array. (...) There are many factors to consider when choosing a sorting algorithm to use.

Resumidamente, é o tipo de algoritmo que tem por entrada um array e organiza os seus items seguindo uma ordem. Um fator a se considerar é que, as dimensões do array, e as limitações de espaço, podem influenciar na escolha do algoritmo que será utilizado.

Bubble sort

O Bubble sort é a escolha mais comum quando começamos a estudar sobre algoritmos e ordenação, por sua simplicidade e por dar uma ideia geral sobre como funcionam tais algoritmos.

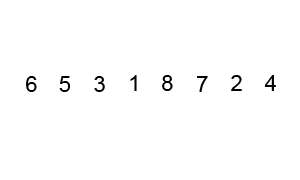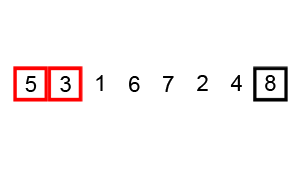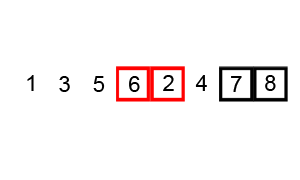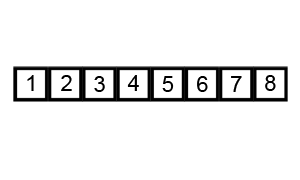
Passos do Bubble sort (wikipedia.org)

Os passos são os seguintes:

Compare A[0] e A[1]. Se A[0] for maior que A[1], troque os elementos;
Vá para A[1]. Se A[1] for maior que A[2], troque os elementos; Repita o processo para cada par de elementos até o final do array;
Repita os passos 1 e 2 n vezes.

E é daí que vem seu nome: Pegue o valor mais alto, e "bubble it up" até o fim do array.

Abaixo o algoritmo representado em código Python:

def bubble_sort(array):
    """
    Teste de mesa
    -------------

    array = []:
        - `i` é `-1`, não cai no laço `while` e retorna array sem modificações

    array = [1]:
        - `i` é `0`, não cai no laço `while` e retorna array sem modificações

    array = [1, 2]:
        - `i` é `1`, entra no laço `while`
        - `range(1)` resulta em `[0]`
        - `j` é `0`. `j[0]` é menor que `j[1]`. Não faz swap
        - Sai do laço `for`
        - `i` é `0`. Sai do laço `while`
        - Retorna array sem modificações

    array = [3, 1, 2, 4]:
        - `i` é `3`, entra no laço `while`
        - `range(3)` resulta em `[0, 1, 2]`
        - `j` é `0`. `j[0]` é maior que `j[1]`. Faz swap
        - `array` fica [1, 3, 2, 4]
        - `j` é `1`. `j[1]` é maior que `j[2]`. Faz swap
        - `array` fica [1, 2, 3, 4]
        - `j` é `2`. `j[2]` é menor que `j[3]`. Não faz swap
        - Sai do laço `for`
        - `i` é `2`, entra no laço `for [0, 1]`. Itens estão ordenados. Não faz swap
        - Sai do laço `for`
        - `i` é `1`, entra no laço `for [0]`. Itens estão ordenados. Não faz swap
        - `i` é `0`. Sai do laço `while`
        - Retorna array ordenado
    """
    def swap(i, j):
        array[i], array[j] = array[j], array[i]

    i = len(array) - 1
    while i >= 0:
        for j in range(i):
            if array[j] > array[j + 1]:
                swap(i, j)
        i -= 1

    # Ao alterar o array in-place, não há reais motivos para retorná-lo
    return array

Running-time complexity: Para cada elemento do array, o algoritmo faz n - 1 comparações. Considerando que ele percorre todo o array fazendo n - 1 comparações, em big O notation temos O(n^2).
Space complexity: Como operamos a troca de elementos (swap), não precisamos de nenhuma outra estrutura de dados para armazenar o resultado da operação, com isso, temos complexidade de espaço de O(1).

Selection sort

Outro algoritmo simples e intuitivo, e ligeiramente mais performático, é o Selection sort.

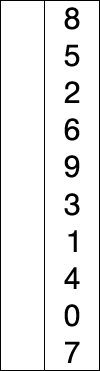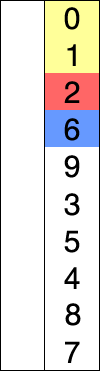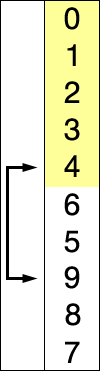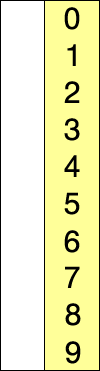
Passos do Selection Sort (wikipedia.org)

Os passos podem ser resumidos em:

Encontre o menor valor;
Troque o menor valor com o primeiro item do array;
Encontre o segundo menor valor;
Troque o segundo menor valor com o segundo item do array;
Repita a operação até o array estar ordenado.

Image do filme MadMax — Um mundo sem ordem é um mundo infeliz (tasteofcinema.com)

No algoritmo anterior tínhamos como finalidade mover o maior valor para o final do array. Nesse, a finalidade é selecionar o valor mais baixo no array, e movê-lo para o começo da estrutura.

def selection_sort(array):
    """
    Teste de mesa
    -------------

    array = []:
        - `len(array)` é `0`, não cai no primeiro no laço `for` e retorna array sem modificações

    array = [1]:
        - `len(array)` é `1`, entra no primeiro laço `for`
        - `min_index` é `0`, não entra no segundo laço
        - Retorna array sem modificações

    array = [1, 2]:
        - `len(array)` é `2`, entra no primeiro laço `for`
        - `i` é `0` e `min_index` é `0`. Entra no segundo laço `for`
        - `j` é `1`. `array[0]` não é maior que `array[1]`
        - Sai do segundo laço `for`
        - Faz swap `0` (`i`) e `0` (`min_index`)
        - Retorna array sem modificações

    array = [3, 1, 2, 4]:
        - `len(array)` é `4`, entra no primeiro laço `for`
        - `i` é `0` e `min_index` é `0`. Entra no segundo laço `for`
        - `j` é `1`. `array[0]` é maior que `array[1]`
        - `min_index` é `1`
        - `j` é `2`. `array[1]` não é maior que `array[2]`
        - `j` é `3`. `array[1]` não é maior que `array[3]`
        - Sai do segundo laço `for`
        - Faz swap `0` (`i`) e `1` (`min_index`)
        - `array` fica [1, 3, 2, 4]
        - `i` é `1` e `min_index` é `1`. Entra no segundo laço `for`
        - `j` é `2`. `array[1]` é maior que `array[2]`
        - `min_index` é `2`
        - `j` é `3`. `array[2]` não é maior que `array[3]`
        - Sai do segundo laço `for`
        - Faz swap `1` (`i`) e `2` (`min_index`)
        - `array` fica [1, 2, 3, 4]
        - `i` é `2` e `min_index` é `2`. Entra no segundo laço `for`
        - `j` é `3`. `array[2]` não é maior que `array[3]`
        - Sai do segundo laço `for`
        - Faz swap `2` (`i`) e `2` (`min_index`)
        - `i` é `3` e `min_index` é `3`. Não entra no segundo laço `for`
        - Faz swap `3` (`i`) e `3` (`min_index`)
        - Sai do primeiro laço `for`
        - Retorna array ordenado
    """
    def swap(i, j):
        array[i], array[j] = array[j], array[i

    for i in range(len(array)):
        min_index = i
        for j in range(i + 1, len(array)):
            if array[min_index] > array[j]:
                min_index = j

        swap(i, min_index)

    # Ao alterar o array in-place, não há reais motivos para retorná-lo
    return array

Running-time complexity: Ao percebermos os dois loops alinhados, percorrendo a dimensão do array cada, podemos concluir que a complexidade é de O(n^2).
Space complexity: Como operamos a troca de elementos (swap), não precisamos de nenhuma outra estrutura de dados para armazenar o resultado da operação, com isso, temos complexidade de espaço de O(1).

Insertion sort

Para finalizar essa primeira parte do artigo, apresentamos o Insertion sort.

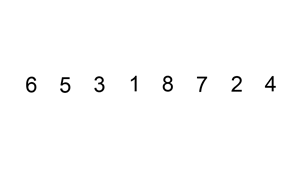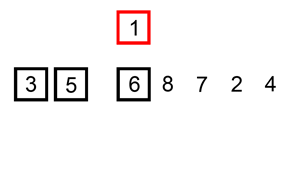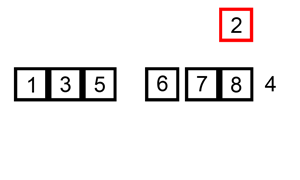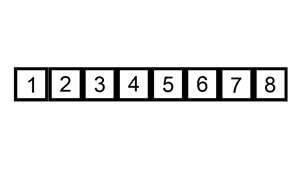
Passos do Insertion sort (wikipedia.org)

Embora ele se compare aos dois algoritmos acima em running time, na minha opinião, imaginar o seu funcionamento demanda um pouquinho mais de esforço. Nesse algoritmo, o propósito é achar o lugar onde o elemento deveria estar no array:

Para cada elemento A[i];
Se A[i] > A[i + 1];
Troque os elementos até A[i] <= A[i + 1].

Abaixo a implementação em Python:

def insertion_sort(array):
    """
    Teste de mesa
    -------------

    array = []:
        - `len(array)` é `0`, não cai no laço `for` e retorno array sem modificações

    array = [1]:
        - `len(array)` é `1`, mas `range(1, len(array))` resulta em `[]`
        - Retorna array sem modificações

    array = [1, 2]:
        - `len(array)` é `2`, entra no laço `for`
        - `slot` é `1`. `value` é `2` e `test_slot` é `0`
        - `test_slot` é maior que `-1`, mas `array[0]` não é maior que `2`
        - `array[1]` recebe `2` (mesmo valor)
        - Retorna array sem modificações

    array = [3, 1, 2, 4]:
        - `len(array)` é `4`, entra no laço `for`
        - `slot` é `1`, `value` é `1` e `test_slot` é `0`
        - `test_slot` é maior que `-1` e `array[0]` é maior que `1`. Entra no laço `while`
        - `array[1]` recebe `array[0]`
        - `test_slot` é `-1`
        - `array` fica [3, 3, 2, 4]
        - `test_slot` não é maior que `-1`. Sai do laço `while`
        - `array[0]` recebe `1`
        - `array` fica [1, 3, 2, 4]
        - `slot` é `2`, `value` é `2` e `test_slot` é `1`
        - `test_slot` é maior que `-1` e `array[1]` é maior que `2`. Entra no laço `while`
        - `array[2]` recebe `3`
        - `test_slot` é `0`
        - `array` fica [1, 3, 3, 4]
        - `test_slot` é maior que `-1`, mas `array[0]` não é maior que `2`. Sai do laço `while`
        - `array[1]` recebe `2`
        - `array` fica [1, 2, 3, 4]
        - `slot` é `3`, `value` é `4` e `test_slot` é `2`
        - `test_slot` é maior que `-1`, mas `array[2]` não é maior que `4`. Não entra no laço `while`
        - `array[3]` recebe `4` (mesmo valor). Sai do laço `for`
        - Retorna array ordenado
    """

    for slot in range(1, len(array)):
        value = array[slot]
        test_slot = slot - 1

        while test_slot > -1 and array[test_slot] > value:
            array[test_slot + 1] = array[test_slot]
            test_slot = test_slot - 1

        array[test_slot + 1] = value

    # Ao alterar o array in-place, não há reais motivos para retorná-lo
    return array

Running-time complexity: No melhor cenário, o algoritmo terá complexidade O(n). O mesmo apresenta complexidade O(n^2) como pior cenário.
Space complexity: Como operamos a troca de elementos (swap), não precisamos de nenhuma outra estrutura de dados para armazenar o resultado da operação, com isso, temos complexidade de espaço de O(1).

Considerações finais

Os algoritmos listados nesse artigo não possuem performance atrativa, mas são a escolha perfeita para introduzir o conceito de algoritmos e ordenação de elementos. E por mais que você sinta-se tentado a defender a ótima característica de space complexity que eles possuem, ainda assim há soluções mais práticas para os problemas de ordenação do cotidiano.

Nos próximos artigos vamos explorar algumas delas, como o Merge e Quicksort.

Referências

estrutura-de-dados ordenacao algoritmos